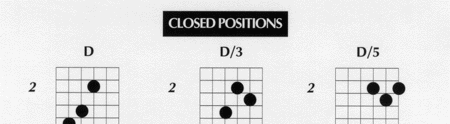
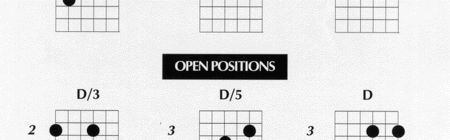
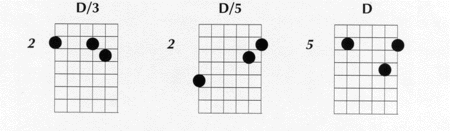
|
PEDAL
POINT
by Dick Grove
The term ‘Pedal Point’ is a traditional term that
refers to a special organization of two musical ideas played against
each other. We will find that this event is common to all styles of
music, and in all varieties of orchestral possibilities from solo
piano or guitar to full symphonic orchestras.
You may be
familiar with this device, or perhaps only vaguely aware of it.
Suffice to say, it helps to be knowledgeable about useful musical
effects such as this, and that is the reason for this article. The
subject is not discussed too much, and we can’t assume everyone
understands the ‘pedal’ or can create one at will.
Here is a
simple way to identify and appreciate a ‘Pedal’ or ‘Pedal Point’ as
used in contemporary musical styles.
A Pedal Point
is:
| a. |
Two musical ideas played against each
other |
| b. |
Of the two, one is of primary importance and
the other is secondary to the primary idea |
| c. |
The primary idea is always some treatment of a
given melody |
| d. |
The secondary idea is a tonally simple element
based on the tonality of the key signature or of a momentary
key center within the composition |
| e. |
The trick to having two ideas playing
simultaneously is that the rhythms of the ideas need to be
‘staggered’ (i.e. attacking at different
times) |
Here is how one constructs a typical Pedal Point:
| a. |
The primary element of the melody
can be treated in any of the following ways: |
|
1. |
as a solo instrument or instruments playing in
unison or octaves |
|
2. |
a harmonized treatment of the melody with the
style of harmonization based on the musical style in which the
effect is used. This means that in a big band jazz style, the
melody could be fully harmonized with a brass section of
trumpets trombones. It can be from 3-part to 8-part
harmony |
|
3. |
the melody can be supported without chords,
but with ‘shapes’ or ‘couplings’ placed under the melody. A
coupling is where a set interval configuration moves parallel
to the
melody in a strict consistent fashion |
|
4. |
as an improvised solo (in any style) against
the pedal |
| b. |
The Pedal is a repeated tone, played
rhythmically against the melody. It has these
characteristics: |
|
1. |
the repeated tone is either ‘SO’ or the 5th of
the given tonality or ‘DO’ of the tonality |
|
2. |
by repeating the tone, the tonality is
‘grounded’ in a very basic manner, which to the ear firmly
establishes the key center. This then allows the character of
the melodic
treatment be quite dissonant and still
musically acceptable |
|
3. |
a pedal can be orchestrated for any
instruments. The most common is with low-pitched instruments
like the tympani, trombones, baritone saxophone, celli, low
register keyboard and all low synth patches. On the
other hand, high unison violins are commonly used for a pedal
‘hanging effect’ on ballads,
etc. |
As there are pedals based on SO or DO of a key center,
their use is usually based on this reasoning:
| a. |
when a chord progression of the section to be
treated as a pedal has the character of being primarily
in one key center, SO is the optimum scale degree tone to
use |
| b. |
when a chord progression modulates frequently,
then DO is the more effective of the two
possibilities |
There is also the idea of using both SO and DO as a
pedal. We can refer to this as a ‘Double Pedal’ In this context, the
typical usage is to create a bass pattern alternating from the low
DO to the SO above, on up to the high DO, then back to the SO and
down to the low DO. This is used as a bass part in a rhythm section
or as the left hand of a piano or keyboard part.
As an
example of how dissonance can be used against a pedal, play the
following illustrations:
Example 1
USING ‘SO’ AS A PEDAL
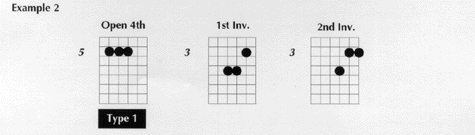
Example 2
USING ‘DO’ AS A PEDAL
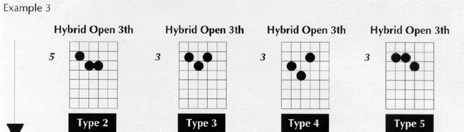
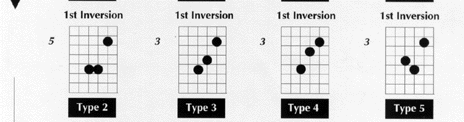
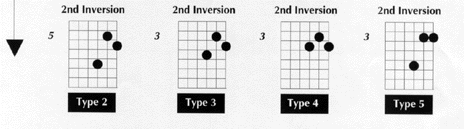
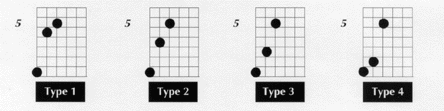
Example 3
USING A DOUBLE PEDAL
Listen the next time to a treatment of music utilizing the
Pedal Point effect, and try to appreciate the dramatic effect it
creates. The tension that comes from the harmonic clashes between
the two musical elements can build a climatic peak (bringing a high
contour to the section of music it is found in) or sustain a
sophisticated degree of tension in a soft, introspective mood. The
difference is a matter of the orchestral limits available, or the
overall impression desired by the players or writers.
For a
pianist, it provides a relatively simple device to play seemingly
complicated rhythms and harmonic ideas by each hand playing one
element and staggering the rhythms in a natural ‘ear’ approach. It
provides a way to imply fast tempos with a minimum of physical
demands.
Thanks for joining us in our discussion, hope it
helps you!
Dick Grove
|
|
THE REAL CIRCLE OF
5th'S
by Dick Grove
One of the time honored foundations of contemporary
music is called the Circle of 5ths. It is taught in countless theory
books, schools, universities and by private teachers. Yet you would
be surprised at how many different interpretations of this term you
would hear if you asked a sampling of musicians.
The
traditional approach is to diagram a series of key centers moving
like the hours of a clock, some starting at ‘noon’ with the key of C
then to F, Bb, Eb, Ab, Db, etc ending up with D to G and back to C,
moving clockwise. On the other hand the presentation might be in
reverse, starting at C then to G, D, A, E, etc., ending up with Bb
to F and back to C, moving clockwise.
Either diagram can then
be seen moving clockwise or counterclockwise. Now we are in
business, so to speak, because we have the vaunted, Circle of 5ths.
Or is it called the Circle of 4ths? or which is which – and why is
either one the way it is? Some good questions! And all the diagrams
and different ways to look at this relationship do not explain what
is really going on with this relationship of tonal centers, much
less how to relate to this important foundation in the music we make
everyday.
At first glance it would seem that the point of
this information is to establish a basic relationship that is an
integral part of our music, from Bach to the present. However
critical questions remain to be understood from an intellectual
point of view, and more importantly, from a musical intuitive
standpoint.
This article will attempt to explain what is
really going on with this series of tones, and how to see and hear
it ‘in action’ in our music. First of all we need to see that if we
are discussing tonal key centers, we have to first know how a key
center is created. What relationship, when heard, tells our ear what
the key actually is.
The presumption also is that the Circle
of 5ths is stating that the key at ‘noon’ on the clock, then changes
or modulates to the key at 1:00 , and then to 2:00 etc. So it really
is a concept that tries to explain a natural order of modulations
from one key to the next in a prescribed order rather than a random
order. This is an important starting point to understanding why we
are even discussing this to begin with!
Theoretically, any
key center can modulate to any other key center at any time.
Therefore the importance of the Circle of 5ths is that it represents
the most natural relationship between momentary key centers.
The basis of this relationship, and the factor that defines
a tonality to our ear is a 4-note sequence of tones called a
tetrachord. The term ‘tetra’ stands for four, and within the
interval of a perfect 4th (i.e. C to F) there will be two more
tones, connecting the C to the F. This particular tetrachord is
termed a Major Tetrachord. Along with this relationship we
need to understand that the interval formula of this Major
Tetrachord is whole step, whole step, half step or 2 + 2 + 1 (using
half steps) The half step in each tetrachord is the defining
interval to our ear, because the interval of a half step leads to
the next tone. It is termed an active half step in context to a
tonality and defines to the ear where the tone will naturally
resolve.
Now we know that in a ‘C’ major scale we have seven
tones, When we look at the major scale from a tetrachord standpoint
we find a tetrachord starting on DO or 1, and a second tetrachord
starting on SO or 5. These two major tetrachords therefore build
your major scale.
The conclusion is that what we think of as
our common major scale, is actually two Major tetrachords linked
together, giving us 8 tones instead of the 7 literal letternames.
This means we have a high DO and a low DO. The Major tetrachord is
the building block of the major scale and hearing a
tonality!
Check out the following Example 1:
The upper tetrachord in relation to a major tonality
can be thought of asThe upper tetrachord in relation to a major
tonality can be thought of as the 5th, 6th, 7th degrees of a major
scale, ending on the octave; (or 8) In solfege, this would be SO,
LA, TI to DO. The diatonic half step is the TI resolving to DO, an
ascending resolution that makes a distinct impression to our
ear.
The lower tetrachord in relation to a major tonality can
be thought of as the 4th, 3rd and 2nd degrees of a major scale,
ending on the octave; (or tonic of the scale) In solfege, this would
be FA, MI, RE to DO. The diatonic half step is the FA resolving to
MI, an descending resolution that also makes its distinct impression
when we hear it.
Any two of these building blocks, starting
on the next tone a perfect 5th above or below the last starting
note, create our major scale. There are some interesting
observations that become very clear, namely that each tetrachord can
be found in two major scales. This means that the lower tetrachord
of a C scale has the same notes as the upper tetrachord of a F
scale. They are therefore all interlocking.
This series of
ascending or descending tetrachord segments reflect the ascending
resolution of the TI - DO diatonic half step or the descending
resolution of the FA - MI diatonic half step. Depending on which
tetrachord you choose, you will create a series of key centers, each
of which are exactly a perfect 5th from each other.
| THE MELODIC
CIRCLE of
5ths |
The point of all of this explanation and the
subject of this article, is that there is in reality, TWO Circles of
5ths. One is called the Melodic Circle of 5ths and the other, the
Harmonic Circle of 5ths. We will discuss the Melodic Circle
first.
As the SO, LA, TI to DO ascending tetrachord moves up,
we can start at the bottom of the piano keyboard, and sequence up,
each time starting a new tetrachord on the tone a Per 5th above the
last starting tone. If you follow this sequence all the way to the
top of the keyboard, you will have created a Circle relationship of
key centers that move starting on the lowest G (SO in the key of
‘C’) of the keyboard through all 12 possible key centers, and ending
in the key of ‘C’ at the top of the keyboard. Each two consecutive
tetrachords produce first the C major scale, then the G, the D, A,
E, B(Cb), F#(Gb), C#(Db), Ab, Eb, Bb, F, and finally C again. The
reason we call this the Melodic Circle of 5ths is that the changes
of key centers will sound natural and satisfying melodically - but
not harmonically if you have any harmonic chord forms larger than a
triad.
You will find this modulation of key centers
typically in pop and rock songs, using mainly only 3-part triadic
solutions for chord progressions. You will also find the sequence in
early classical music in a time period where the style would permit
only triadic chords, the old IV - V - I harmonies of religious and
baroque styles of music.
| THE HARMONIC
CIRCLE of 5ths
|
When the FA, MI, RE to DO descending
tetrachord moves down, we can start at the top of the piano
keyboard, and sequence down, each time starting a new tetrachord on
the tone a Per 5th below the last starting tone. If you follow this
sequence all the way to the bottom of the keyboard, you will have
created a Circle relationship of key centers that move starting on
the highest C (FA in the key of ‘G’) of the keyboard through all 12
possible key centers, and ending in the key of ‘C’ at the bottom of
the keyboard. Each two consecutive tetrachords produce first the C
major scale, then the F, the Bb, Eb, Ab, Db(C#), Gb(F#), Cb(B), E,
A, D, G and finally C again. The reason we call this the Harmonic
Circle of 5ths is that the changes of key centers will sound natural
and satisfying harmonically - and the chord forms can be as dense as
an 8-part altered dominant chord! This is musically natural, as the
active scale degrees that have the tendency to resolve down, will
always be moving to the needed tone in the next key center. You will
find this modulation of key centers typically in all standards, many
pop tunes, jazz, latin, and all styles that have sophisticated
melodies. This enables the music to have the greatest amount of
possibilities and therefore the most unique and memorable
impressions!.
The next examples illustrate the overlapping
tetrachords, and are labeled in terms of the solfege syllables. All
circled note names function as DO of that specific momentary key
center.
Example 2
Example 3
The upshot of all the above is
that when a musician speaks of the Circle of 5ths, they are
referring to the Harmonic Circle, not the Melodic. The old and
valuable chord progression of C7, F7, Bb7, Eb7 etc, is the Harmonic
Circle using the V7 chord of each key center in the sequence of FA,
MI, RE to DO.
You should be aware of are that this most
natural of all modulations from key to key is driven by natural
resolutions of FA to MI, and TI to DO. It is the story of the
half step or the absence of the half step from beginning to
the end.
Notice how the interval makeup of the tetrachord
(2-2-1) creates all of the accidentals of the major keys. Each
tetrachord starting on FA adds the flat of the next flat key
signature (1 flat to 7 flats). Each tetrachord starting on SO ends
with TI - DO, with the TI being the added sharp for each new sharp
key signature (1 sharp to 7 sharps).
|